STDEV.P／STDEV.S（スタンダードディービエーション・ピー／エス）関数の使い方

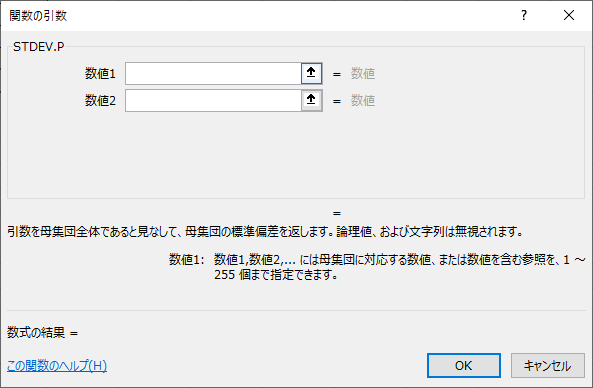
STDEV.P（スタンダードディービエーション・ピー）関数のPは、ポピュレーション（母集団）を意味し、母集団に対しての標準偏差を求めます。

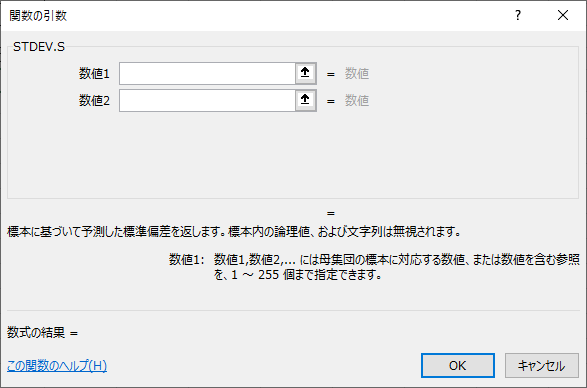
SEDEV.S（スタンダードディービエーション・エス）関数のSは、サンプル（標本）を意味し、標本に対して、母集団の標準偏差を推定する標準偏差を求めます。

【構文】

＝STDEV.P(数値1, 数値2……)

＝STDEV.S(数値1, 数値2……)

【使用例】

• ＝STDEV.P(B2:B100)
  セルB2～B100までの数値データの標準偏差を計算します。
• ＝STDEV.S(B2:B100)
  セルB2～B100までの数値データで、母集団を推定する標準偏差を計算します。

[char no=”1″ char=”さえちゃん１”]標準偏差を勉強する際には、必ず分散のVAR関数をしっかりと学習してください。VAR関数の平方根がSTDEV関数の値になります。そのため、分散同様、母集団の標準偏差、標本の標準偏差（標本標準偏差）、不偏標準偏差と使い分けがあります。[/char]

関数説明

分散で説明したときのデータを使いましょう。セルE5には、VAR.P関数が入っています。

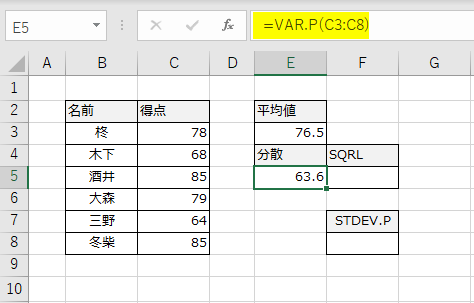
これをSQRL関数で平方根を出力してみます。

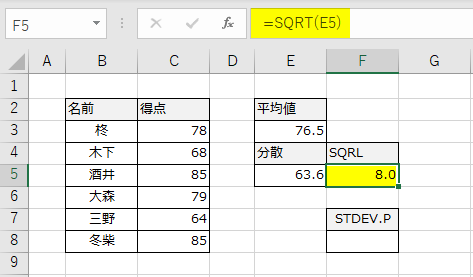
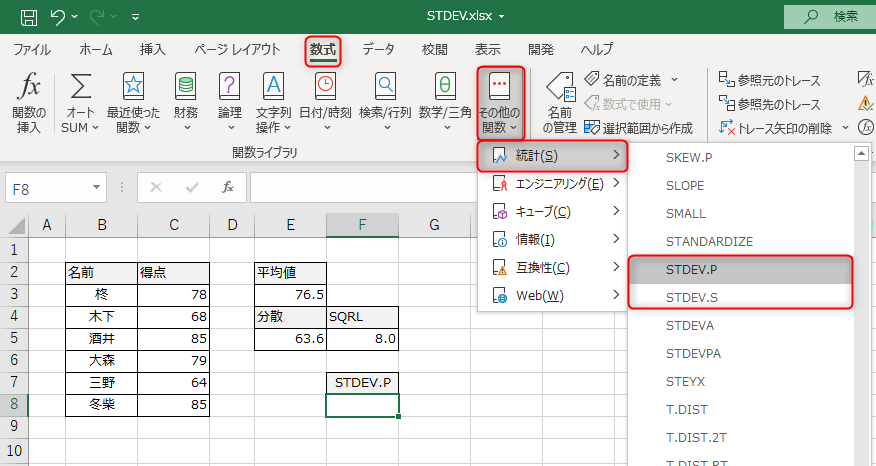
分散の平方根が標準偏差になります。この作業をSTDEV.P関数を使って求めてみましょう。この関数は、[数式]タブ→関数ライブラリ[その他の関数]→[統計]の中にあります。

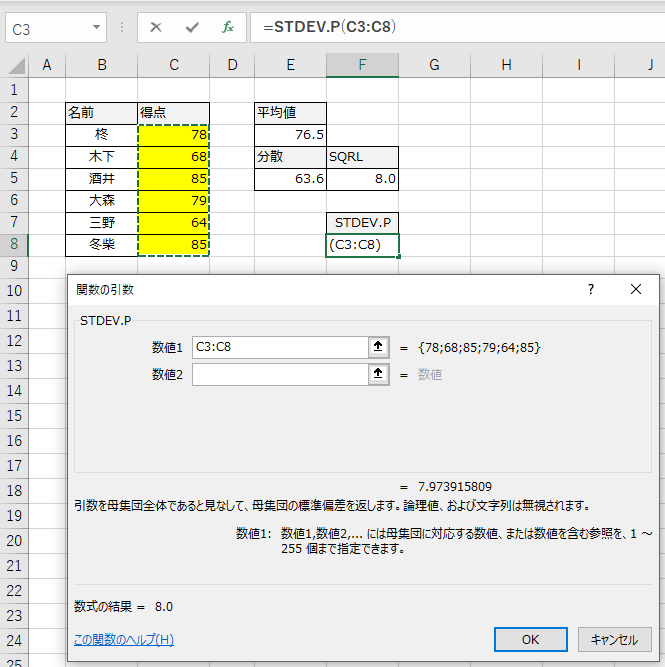
使い方は、SUM関数と同じです。標準偏差を出したい範囲を選択します。

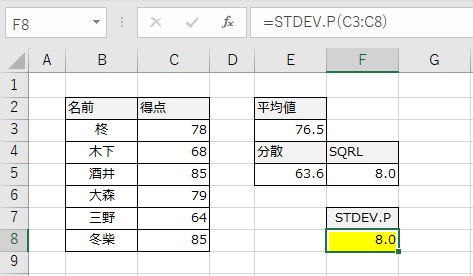
これで先ほどと同じ数値が出ました。

繰り返しになりますが、STDEV.PとSTDEV.Sの違いは、VAR関数の理解が鍵となります。

STDEV関数は、標準偏差という結果をすぐに出力してしまうので、標準偏差を出力するための計算フローを知らずに使用した場合、誤った使い方をしてしまいがちです。

使用するデータにSTDEV.PとSTDEV.Sどちらが適切か？　は、しっかりと考えて使ってください。

さえちゃんのSTDEV.P SEDEV.S関数ワンポイントアドバイス

[char no=”4″ char=”さえちゃん３”]標準偏差で出力される値を「σ（小文字のシグマ）」で表します。１σには約68％のデータが集まっていて、２σには約95％、３σには約99％のデータが含まれているよ～というのは暗記しちゃってください。[/char]

標準偏差を学習するときは、こちらの正規分布を思い描いてください。中心を平均値として前後の-1.0 ＋1.0 の範囲が、標準偏差の-１σ＋１σの範囲になります。

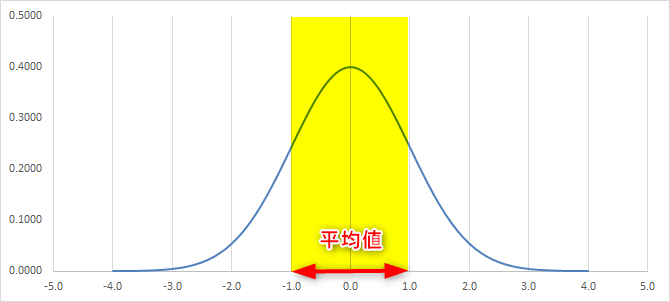
つまり、平均が「70」で、標準偏差が「5」と出力された場合は、65～75の間にデータが約68％ありますよ～という意味になります。

もちろん、データによってはこの山が右寄りだったり、左寄りだったり、凹型のようなふた山型だったりするわけですが、世の中のデータはこの正規分布にだいたい収まるとされています。

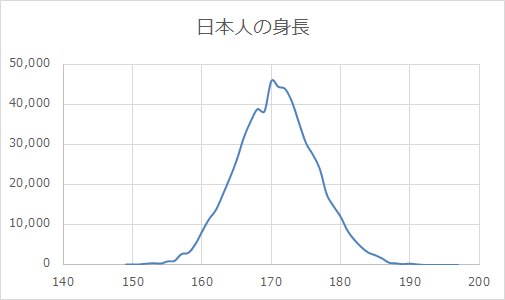
正規分布に収まる代表的なデータは、日本人の身長です。

総務省からひっぱってきたデータを整理してまとめると、身長167cm～168cmの凹みはすこし気になりますが、先ほどの正規分布とよく似ています。

こういう情報がわかると、例えば、S・M・Lサイズの洋服はどのくらい作ればいいのか？　とか、座席シートの設計の際にどの程度の空間があればリラックスできるのか？　とか、そういった業務における最適なアクションがとれるようになりますよね。

データから情報を読み取る作業フローは、このような感じです。

関数ステータス

関数ライブラリの種類

統計

数式の構文

＝STDEV.P(数値1, 数値2……)

＝STDEV.S(数値1, 数値2……)

引数ダイアログ

Microsoft 公式サポート

STDEV.P関数 – Office サポート

STDEV.S関数 – Office サポート

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2024年は、佐賀県に行って「呼子のイカ」を思いっきり食べたいです。

引き続き、青森・秋田・岩手でのお仕事ご依頼、お待ちしております！