COVARIANCE(コバリアンス)関数の使い方

関数概要
COVARIANCE(コバリアンス)関数は、データの関係の深さを表す指標(共分散)を出力します。末尾につくのが「P」の場合は母集団データに対して、「S」は標本データに対して使用します。
【構文】
=COVARIANCE.P(or S)(数値1, 数値2……)
【使用例】
- =COVARIANCE.P(or S)(B2:B100,C2:C100)
セルB2~B100のデータ群と、セルBC~C100までのデータ群の共分散を出力します。 - =COVARIANCE.P(or S)(B:B,C:C)
上記範囲は、セル結合やその他の表がなければ、列単位でも取得が可能です。
[char no=”1″ char=”さえちゃん1”]標準偏差を求めるために説明した VAR(バリアンス)関数のように、通常はこの関数を使う機会はありません。この関数は、2つのデータの関係性を知る「相関係数」という指標を知るうえでは、避けては通れない重要な関数となります。統計解析で用いる関数は、答えを一気に算出してくれますが、計算フローをちゃんと把握することが重要です。[/char]
YouTube説明
関数説明
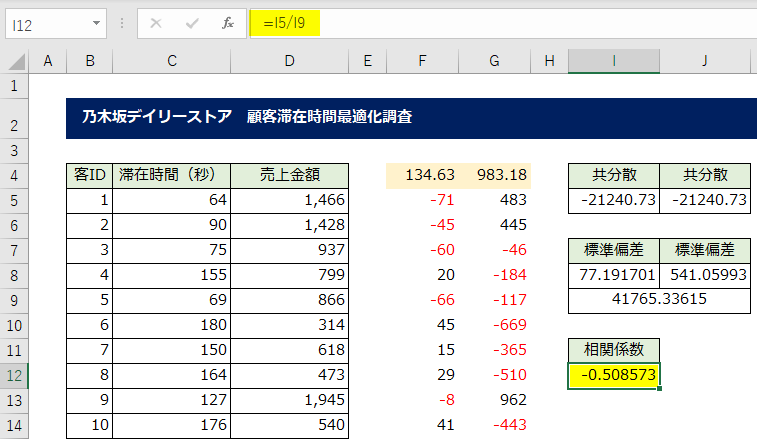
2つのデータの関係性の深さを示す「共分散」を求めてみましょう。サンプルデータは、架空の店舗「乃木坂デイリーストア」の顧客滞在時間と、売上金額をまとめたものです。
[滞在時間]と[売上金額]に関係性があるのかを調べてみます。画面キャプチャの表示上は、8件しか表示されていませんが、実際は100件あります。
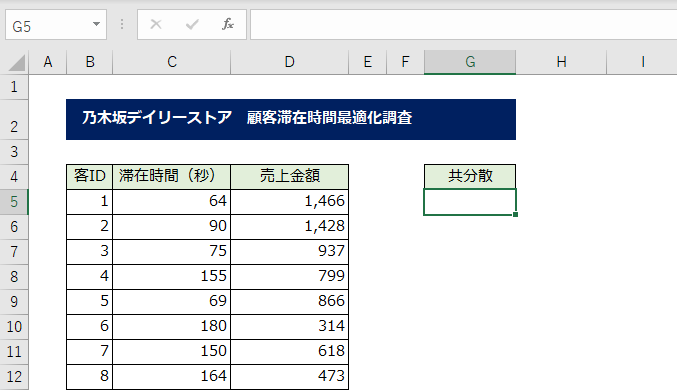
この100件のデータは、無作為に抽出したデータとなりますので、乃木坂デイリーストアの最適化調査に扱う「標本データ」として扱っていきます。
COVARIANCE関数は、[数式]タブ→関数ライブラリの[その他の関数]→[統計]の中にあります。
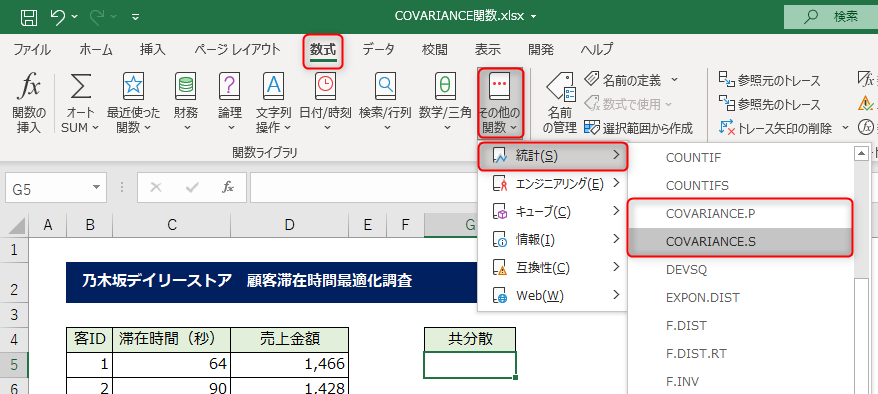
今回は標本データを扱うため、COVARIANCE.Sを使います。
サンプルデータのワークシートは、[滞在時間]と[売上金額]しかデータが存在していないため、ここは簡素に数式を立てるべく、列単位で範囲を取得しましょう。
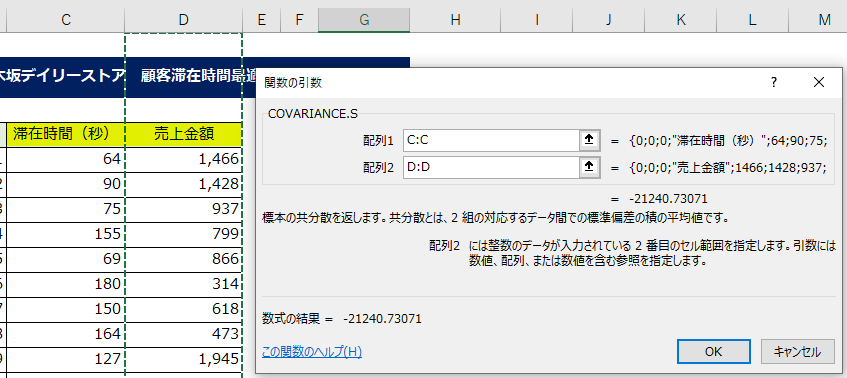
2つのデータ配列を選択するだけで、そのデータの共分散の値が出てきました。
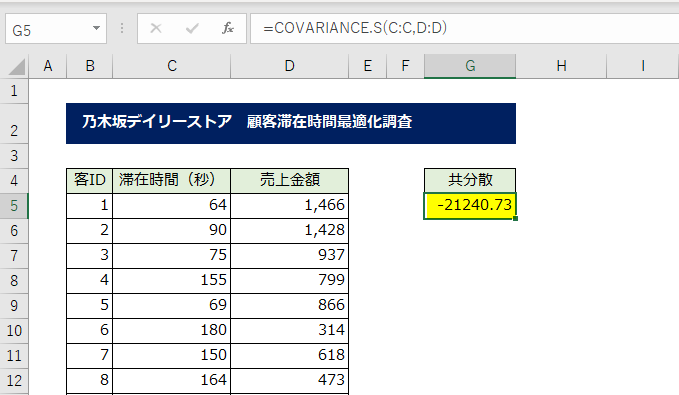
このデータが共分散の値で、データ間の関係の深さを示してくれる値なのですが、滞在時間と売上金額の単位が入ってしまっているため、読みづらい値となってしまっています。
実際の業務では、このデータだけでは関係が深いか浅いかを判別できないので、この共分散の値より単位を取り除く作業が発生します。
次のワンポイントアドバイスで、COVARIANCE関数を使った ① 共分散を導くまでの求め方と、② 共分散後の求め方 を記載しましたので、ぜひご確認ください。
さえちゃんのCOVARIANCE関数ワンポイントアドバイス
[char no=”4″ char=”さえちゃん3”]データを分析するためには、データをしっかりと料理しないといけません。そのためには、料理の仕方をしっかり覚えておく必要があります。相関係数は、データをどう料理したら出てくるか? CORREL関数を使えば一撃で求まりますが、きちんと出力結果までの流れを知っておく必要があります。[/char]
共分散の求めるフロー
① 各データ配列の[滞在時間]と[売上金額]の平均をそれぞれ求めます。
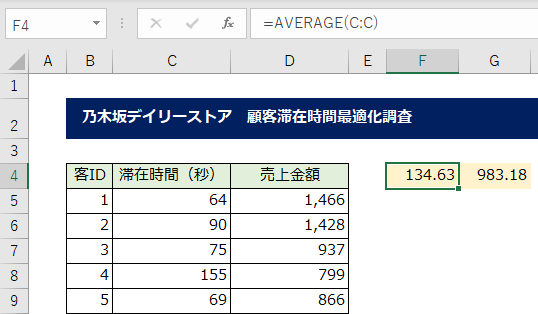
100件分の[滞在時間]の平均は134.63秒、[売上金額]の平均は983.18円と算出されました。
② 各「実データ」-「平均」で偏差を求めていきます。
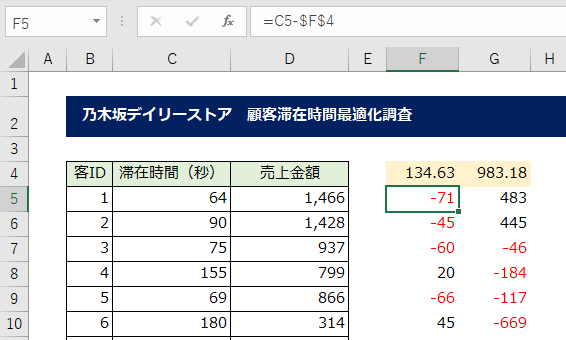
偏差とは、平均からの距離を示しており、客ID「1」番は滞在時間は平均から「-71」秒早く、売上金額は「+483」円高いことがわかります。
この値が偏差になります。それぞれ100件ずつの偏差を出力します。
③ SUMPRODUCT関数で、偏差の各列で集計し、組数で割ります。
母集団の場合は、実データの組数で割り算をし、標本の場合は、実データの組数から「-1」した値で割り算をします。
これはそういうものだ、とこの関数紹介ページでは理解してください。
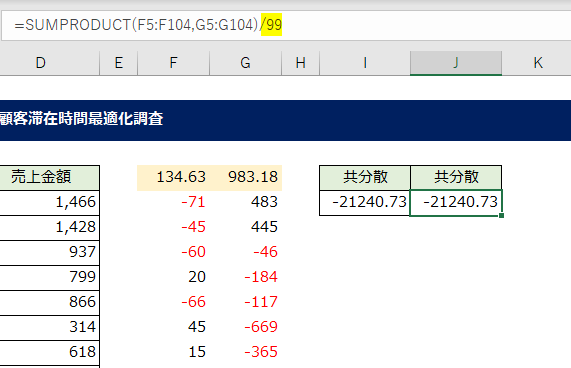
ここでいう組数とは、
「-71」×「483」 1組
「-45」×「445」 2組
「-60」×「-46」 3組
・
・
・
を指しています。データが100件あるので、100組ありますよね。
SUMPRODUCT関数は、この各組の掛け算で出力した値をすべて合算する関数です。
母集団の場合なら、SUMPRODUCT関数で求めた値を「100」で割り、標本の場合ならマイナス1した「99」で割ります。これが共分散を求めるフローです。
結果、COVARIANCE関数と同じ値を導くことができました。
共分散から単位を取り除いて相関係数を導くフロー
[滞在時間]のデータ列と、[売上金額]のデータ列、各データの標準偏差を求めます。
標準偏差を求める関数は、標本なのでSTDEV.S関数を使って求めます。
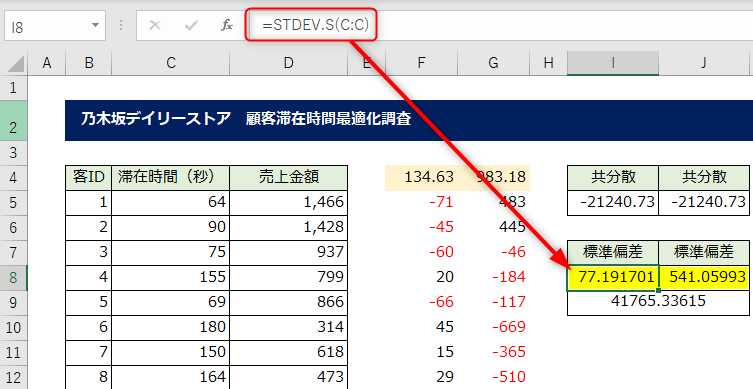
滞在時間の標準偏差と、売上金額の標準偏差、この2つの値を掛け算します。
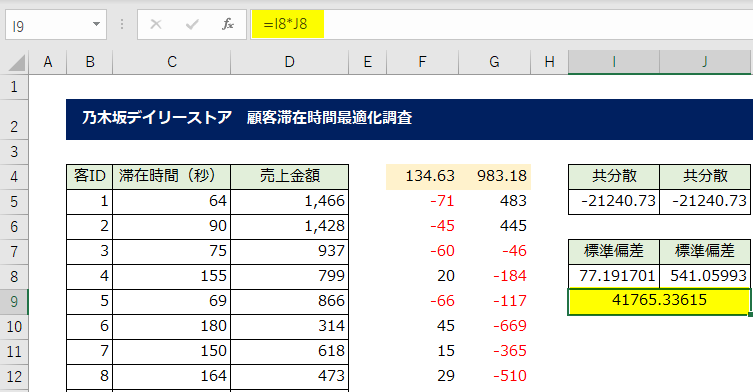
結果「41765.33615」と算出されました。
この値を分母にして、共分散の値で割り算をすれば、データの単位を取り除いた指標、相関係数を導くことができます。
この相関係数が、実際にデータを分析するうえで扱われる値となるのですが、それに関しては相関係数を出力する関数、CORREL関数でご説明します。
まとめると、COVARIANCE関数で算出される共分散は、2つのデータの関係の深さとなる指標ですが、単位が結果に含まれているため、指標ではあるもののこのままでは扱いにくい値となってしまう、ということになります。
分析上は一気に処理が行われるため、この関数を積極的に使うことはありませんが、計算のフローはしっかり関数を使わなくてもできるようにしておくことが重要です。
関数ステータス
関数ライブラリの種類
統計
数式の構文
=COVARIANCE.P (or S)(配列1, 配列2)
引数ダイアログ