ExcelのRAND関数から考える「ランダム」の正体

母集団と標本の記事の中で「単純無作為抽出法」という標本抽出法がありました。

これは「母集団のデータからランダムに選んで標本データを取り出す方法」なのですが、そもそもランダムって何？　と疑問に思ったことはありませんか？

この記事では、私自身が統計を学習して気になっていたテーマ、「ランダムは本当にランダムなのか？」 について、Excel の RAND 関数を使ってご紹介いたします。

RAND関数は０～１までの範囲で乱数を出力する関数です。

ランダムとは何か？

まず、皆さんがイメージしやすい「ランダム」を考えてみましょう。

• 1～100の番号が書かれたボールを1つ選ぶ
• サイコロを振って出た目を見る
• 木から葉っぱがいつ落ちるのかを眺める
• 風の揺らぎを測る
• 雨粒がどこに落ちるかを計測する

こうした自然現象は「予測できない」＝ まさにランダム です。このようなランダムは、自然界がつくり出す本物のランダム と呼ばれます。しかし、問題はここからです。

コンピュータのランダムはどう作られるのか？

私たちは Excel や Python で「乱数」を簡単に出力して扱いますが、コンピュータは本質的には計算をする機械です。自然界のように気まぐれな変化に対応することができません。

つまり、こういう疑問が生まれます。

コンピュータが出す乱数は、本当にランダムなのか？

Excel の RAND(らんだむ) 関数で考えてみましょう。

Excel の RAND 関数

Excel の =RAND() 関数は、引数なしで 0以上1未満のランダムっぽい値 を返してくれます。

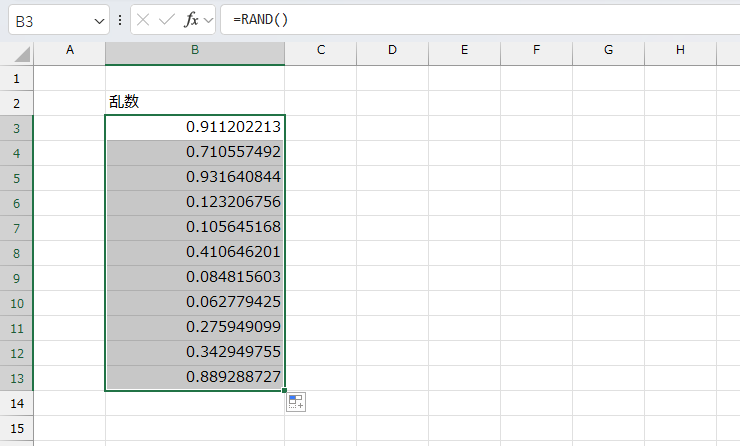
オートフィルで簡単に重複しない値を出力してくれるので、

• 単純無作為抽出のシミュレーション
• グループ分け
• データ分析の練習

など、いろんな場面で利用されています。でも少し考えてみると「どうやって乱数を出力しているの？」 と疑問に思いませんか？

Excel の公式説明には、RAND 関数の内部アルゴリズムは書いていませんが、ヘルプページの関連リンクに Mersenne Twister（メルセンヌ・ツイスター） という世界的に採用されている高品質な疑似乱数アルゴリズムのリンクがありました。

https://en.wikipedia.org/wiki/Mersenne_Twister

Excel2010以降は「Wichmann–Hill 法をベースにしたアルゴリズム」と紹介されている解説が多いですね。ただし、Microsoft は RAND 関数のアルゴリズムを正式には公開していないため、実装は非公開です。

疑似乱数とは？

さて、１つ前のセクションで「ランダムっぽい値」と記載しました。

ですので Excel の RAND 関数のみならず、コンピューターが出力する乱数は、自然界と同じレベルのランダムな数字を出しているわけではありません。

本当の仕組みは、ランダムに見える数字を、計算式で作っているというものです。こうしたものを 疑似乱数（Pseudo Random Number） と呼びます。

疑似乱数例：線形合同法（LCG）

アルゴリズムのイメージを掴むために一番簡単な 「線形合同法（Linear Congruential Generator, LCG）」 という乱数生成式をご紹介します。

式はこうです。

X(n+1) = (a × Xn + c) mod m

各記号の意味：

• Xn：前の乱数
• a：乗数
• c：加数
• m：法（割る数）
• mod：余りを意味する演算

この式をぐるぐる回すだけで、ランダムに見える値が次々に生成されます。あくまで乱数のふりをしているだけ。でも、これが驚くほどよく出来ています。

一番簡単な値の代入で実際にやってみましょう。

線形合同法の最もシンプルな例

パラメータを以下のように設定します。

• a=3
• c=1
• m=7
• 初期値（seed）として、X₀=2 を使用

これで計算してみます。

1回目の乱数生成

X₁ = (3×2+1)  mod  7

計算すると：

• 3 × 2 = 6
• 6 + 1 = 7
• 7 ÷ 7 の余りは 0
• X₁ = 0

2回目の乱数生成

X₂ = (3×0+1)  mod  7

• 3 × 0 = 0
• 0 + 1 = 1
• 1 ÷ 7 の余りは 1
• X₂ = 1

3回目の乱数生成

X₃ = (3×1+1)  mod  7

• 3 × 1 = 3
• 3 + 1 = 4
• 4 ÷ 7 の余りは 4
• X₃ = 4

4回目の乱数生成

X₄ = (3×4+1)  mod  7

• 3 × 4 = 12
• 12 + 1 = 13
• 13 ÷ 7 の余りは 6
• X₄ = 6

5回目の乱数生成

X₅ = (3×6+1)  mod  7

• 3 × 6 = 18
• 18 + 1 = 19
• 19 ÷ 7 の余りは 5
• X₅ ＝ ５

6回目の乱数生成

X₆ = (3×5+1)  mod  7

• 3 × 5 = 15
• 15 + 1 = 16
• 16 ÷ 7 の余りは 2
• X₆ = 2

6回目の乱数作成で無事に循環、最初の値 X₀ = 2 に 戻りました。つまり、この疑似乱数列は、 2→0→1→4→6→5→2→… と変化していきます。

疑似乱数とはこういうものです。Mersenne Twister（メルセンヌ・ツイスター）法は、これがもっと複雑になったものを使っている、という理解で十分だと思います。

疑似乱数で十分かどうか？

結論は 「はい、問題ありません」。

• 統計分析
• 抽選
• シミュレーション
• 無作為抽出
• トレーニングデータによる使用

この程度の用途であれば、疑似乱数で十分すぎる精度です。ランダムと決められた計算式の組み合わせですが、統計学では 疑似乱数＝乱数として扱いで問題ありません。

だから、単純無作為抽出法でもExcelのRAND関数を使っても問題ないことになります。

等しい確率で出力されることを前提にしているため、統計分析や標本抽出には十分な品質なので安心してください。

ただし、暗号化の世界は別

しかし、話が「暗号」になると状況が変わります。

暗号の世界では、巨大な数が「素数であるかどうか」を判定して暗号鍵を生成しますが、その素数をランダムに選ぶためにも「本物の乱数」が使われます。

こうした暗号用乱数は Excel の RAND とはまったく別の仕組みです。

また、暗号の世界では、

• 予測できない
• 再現できない
• 攻撃者が推測できない

といった、完全に予測不能な乱数が必要です。

もし RAND関数の中身や、線形合同法のような計算式がバレると、次に出る乱数が予測されてしまうという致命的な弱点になります。

先ほどの例を挙げると、6の次は5が出るとわかってしまうからです。暗号の世界では、

• ハードウェアによる本物の乱数
• 熱雑音や電気の揺らぎ
• CPUが持つ微小なゆらぎ

などを利用して乱数を作るようになっています。私自身も詳細まではわかりませんが、そういった自然現象による完全なランダムを武器にしないと予測されてしまうでしょう。

これは ExcelのRAND関数とはまったく別の乱数です。

まとめ

今日のポイントを整理すると：

• 自然界には「本物のランダム」がある
• ExcelのRAND関数のようなものは「疑似乱数」である
• しかし、疑似乱数は統計分析や抽選には十分
• 暗号化には、本物の乱数や特殊な乱数生成アルゴリズムが必要
• ランダムの質によって用途がまったく違う

こうして見ると、ランダムも奥が深いですよね。次に RAND 関数を使うときは、ちょっとだけ乱数について思い出してみてください。

最終確認日：2025年11月19日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！