母集団で求める分散と標本で求める分散

私自身、統計学の勉強でとてもハードルが高かったのが「分散」という値の理解でした。まったく理解ができなかった過去があります。

講師である私も沼にはまってしまっていたんですね。

この記事では、分散について勉強していきましょう。

分散を英語で「Variance：ヴァリアンス」と言います。この言葉、響きはかっこいいですが、実際には理解が少し難しいですよね。しかし一度理解できれば、データのばらつきを示す非常に重要な概念だと感じられるはずです！

分散

分散は、２つの用語に分かれます。

母分散は母集団の分散で、標本分散は標本の分散です。まあ、そのままですよね。前の記事で、標準偏差について記載しました。

標準偏差の説明では、まだ母集団と標本というキーワードが登場していなかったため、母集団に対しての計算方法で標準偏差の求め方をご紹介しました。

いまいちど、復習です。

標準偏差とは、データのばらつき、平均値からの １σ の距離を把握し、約68％のデータの範囲を推定する値でした。

その計算過程において、平方根にする前の値「分散」がありました。実はこの分散の算出方法は、対象とするデータが母集団か標本かで求め方が異なります。

標本分散の修正方法

まず、結果からお教えします。

標本データで分散を前述の記事のとおり計算を求めていくと、実際の母集団の分散よりも小さな値で求められてしまうといったデメリットが発生します。

これは、天文学者のフリードリヒ・ヴィルヘルム・ベッセルさんの発見で、このデメリットを解消するために「ベッセル補正」という計算フローが誕生しました。

標本で分散を出力することは、実際の真の分散（母分散）を推定することになります。

求めることができない母分散の推定精度を上げるために、分散の計算式を工夫しないといけないことに気づいたのです。

ただでさえ、分散はスケールが大きな値です。コンピュータのない時代に、昔の数学者はすごいですよね！

それではキャプチャを使って、分散の計算方法を見ていきましょう。

標準偏差の説明に使ったキャプチャを使い回しますので、「分散」の値がどのように計算されたか復習してください。

母集団としての計算方法

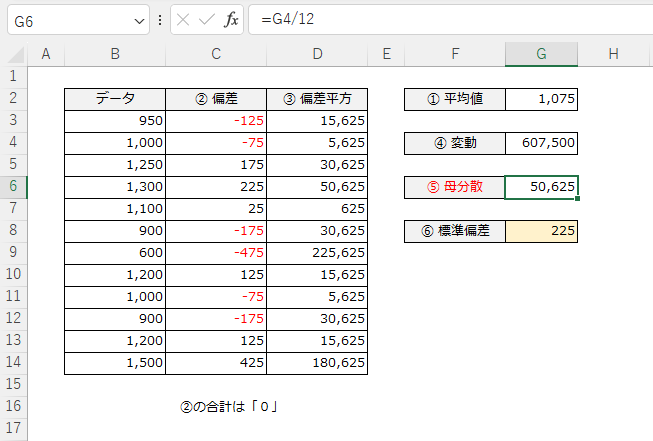
標本における分散の計算補正

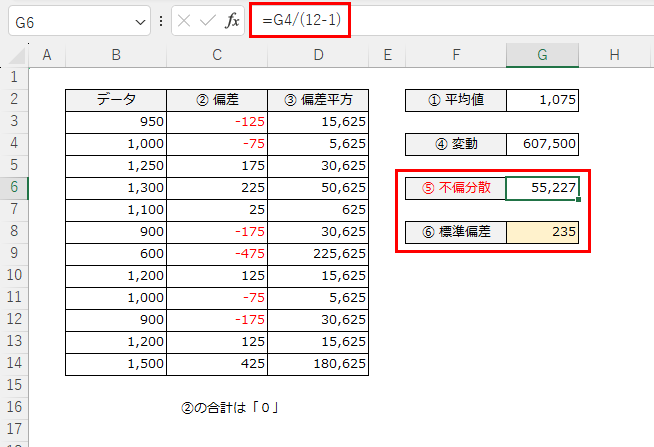
キャプチャのとおり、母分散は変動をデータの件数で割っているのに対し、標本分散の補正は、変動 ÷（データの件数－1）で計算をしています。

分母が減れば、自分の取り分は大きくなるように、分散の値が大きくなりました。

標本分散で、このように補正した分散を、標本に含まれるであろう偏りを取り除いた分散ということで「不偏分散（ふへんぶんさん）」と名付けられました。

なので、「標本分散」は文字通り 「標本の分散」 で、まだベッセル補正をしていない分散のことを指します。「不偏分散」というのが、ベッセル補正の入った分散です。

統計学の最初の勉強で、ここが詰まった箇所です。皆さんはスムーズに覚えられることを祈っています。

どうして１を引くのか？

１を引く理由として、「自由度」というキーワードが関係しています。

自由度とは、自由に選ぶことのできる数のことを意味します。

例えば、5つの桃があったら、自由に選ぶことができる回数は4回ですよね。最後に残った1つは選ぶことができず、必ず残ったものを取得しなければいけません。

このため、自由度は必ず「n-1」となります。

標本データが12個あった場合、自由にデータを選ぶことができる回数は11回です。この「自由に選ぶことができる」という操作を「独立している」と言い換えます。

標本で分散を求める際、独立したデータの件数（自由度）を分母にすることで、実際の母分散に近づくことが発見されました。

だから偏差平方の平均を出力すると考えると、データの件数で割るという定義づけができてしまいますが、偏差平方を自由度（n-1）で割るというのがベッセル補正の正体です。

標本標準偏差とは？

標準偏差も、２つの用語に分かれます。

標本は、標本標準偏差と繋げて言うのですが、母標準偏差とは言いません。きっと、語呂が悪いからでしょう。

母集団に対しての標準偏差は、母分散の平方根で求められます。

標本に対しての標準偏差は、ベッセル補正が組み込まれた不偏分散の平方根で求めるため、母分散で求める計算式より、分散の値がプラスに増加します。

前のキャプチャのとおり、母集団としての計算式では「225」に対し、不偏分散を使った計算式では「235」となったわけです。

この「235」の値の方が、実際の母集団のばらつきに近いということですね。

一般的に、データ分析では標本データを扱うことがほとんどです。ですので、標準偏差を求める場合、不偏分散を扱った計算式を採用するということになります。

ただ、標本数（サンプル数）が多い場合に関しては、結局は母集団に近づいているため、ベッセル補正がなくてもばらつきの差は大したものにはなりません。ですので、ベッセル補正なしで計算をした標準偏差を使っても、さほど大きな問題にはならないでしょう。

まとめ

標本分散・不偏分散・母分散と、統計学の書籍では難解な数式に加えて難しい単語が入り混じるため、標本分散と不偏分散の言葉の違いを独学で完全理解するまで、本当に時間がかかりました。

標本分散と不偏分散の違いは、ベッセル補正あり・なし、だけだったんですね。

分散という値は、標準誤差のときにも使いますし、のちに記載する相関係数を求める際にも使われます。スケールの異なるデータで扱いづらさはありますが、分散は基本統計量の中に含まれる重要な値です。

この分散を確実に理解できると、統計学の視野も広がるはずなので、ここまでの内容を自分の口でも説明できるようにしておきましょう。

専門書籍だと、数式による説明がちんぷんかんぷんで、まったく理解できませんでした。けれども、ようやくここまで計算式を使わないで説明できるようになりました！　皆さんも説明できるくらい理解してくださいね！

最終確認日：2025年11月19日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！