カイ2乗分布表とは？

カイ２乗検定の使い方を前回の記事で学習しましたが、今回はその 検定の中身 をのぞいていきたいと思います。

Excel の CHISQ.TEST 関数はとても便利で、p値まで一瞬で計算してくれます。しかし、その裏側ではどのような仕組みで計算しているのでしょうか？

昔と今を比較しながら、カイ２乗検定の背景を見ていきましょう。

こちらの記事では、データ分析で避けては通れない「困ったデータ」の正体と、その対処方法について学習します。

計算の中身がわかると、カイ２乗検定の仕組みが一気にクリアになるんだけど、一回で無理に覚えようとはしないでね！

カイ２乗値（χ²値）ってどう求めるの？

カイ２乗検定では、次の式で「カイ2乗値（χ²値）」を求めます。

(観測値 − 期待値)² / 期待値

この計算を、クロス表にあるすべてのセルに対して行い、最後に全部足し合わせたものが χ²値です。

イメージとしては、「実際に起きた値（観測値）」が「理論上こうなるはずという値（期待値）」とどれくらいズレているのか？

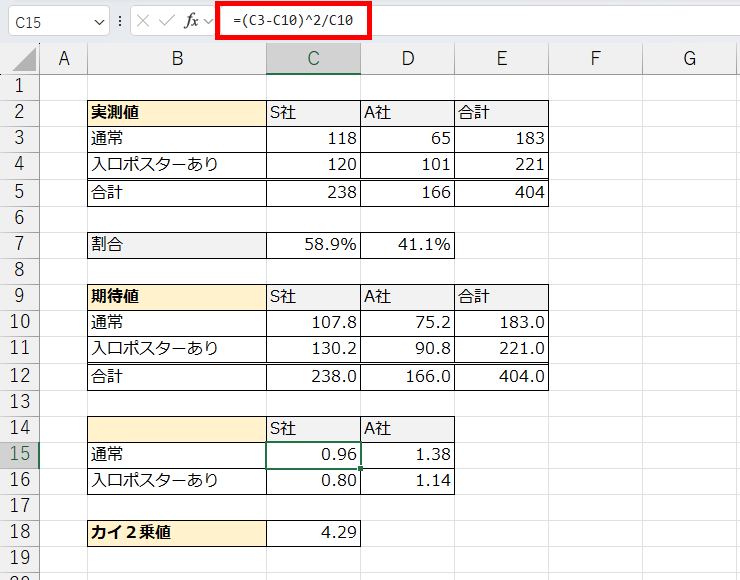
そのズレの大きさを足したのがカイ２乗値です。ズレが大きければ大きいほど、「偶然にしては変だよね？」という判断ができるわけですね。

自由度（Degrees of Freedom）とは？

そして、χ²値が求まったら、次に必要なのが 自由度（Degrees of Freedom） です。クロス集計表の自由度は、次の式で求めます。

• (行 − 1) × (列 − 1)

たとえば、

• 2行 × 2列 の表なら自由度は 1。
• 3行 × 2列 の表なら自由度は 2。

自由度は「データが自由に変動できる数」を表すもので、選ぶことのできる自由だと前の記事でご紹介しましたが、表になるとわかりづらくなるのでそのまま公式を丸暗記するように覚えておいてください。カイ２乗検定では、この値がとても重要になります。

分布表で確認する

次に、コンピューターがない時代のお話です。

昔は、カイ２乗検定の結果が「有意なのか、そうでないのか」は、次のような カイ２乗分布表 を使って判定していました。

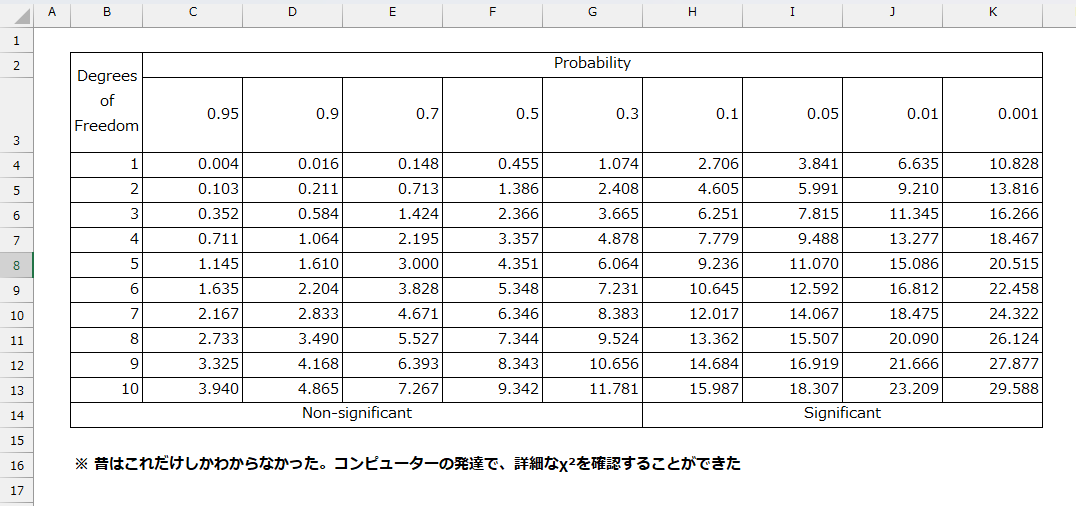
表の見方はこうです。

• 横方向 → 有意確率（0.95、0.05、0.01など）
• 縦方向 → 自由度
• セルの値 → 有意となる境界値

たとえば、自由度 1 の行を見ると、p = 0.05 のところは 3.841 となっています。これは、χ²値が 3.841 を超えていたら、５%水準で「有意」と判断できるという意味です。

つまり昔は、

1. χ²値を自分で計算
2. その値を表で探す
3. 有意かどうかを読み取っていた

というわけなんですね。

昔はこの表が生命線だったんだよ！　みんな手計算でがんばっていたの！

いまはコンピューターが全部やってくれる。現代の分析は言うまでもなく、カイ２乗分布表を手で探す必要はありません。

一応、ここではポスターのデータをカイ２乗値と表で読み取ってみましょう。カイ２乗値が「4.29」だったので、黄色の範囲に入りそうです。

ですから、ｐ値は1％～5％の間、3.841を下回っているので、5％未満であることは表からも読み取れますよね。

５％未満ということは、有意な差がある。つまりポスターの効果があったと言えます。

カイ２乗分布表

CHISQ.DIST関数というものがあります。これで自由度に応じてカイ２乗分布表というものが描けます。

CHISQ.DIST関数に関しては話が長くなるので、こういう分布がコンピューターで描けるんだなという認識で構いません。

曲線は自由度によって変化します。

• 系列１＝自由度１
• 系列２＝自由度２
• 系列３＝自由度３
• 系列４＝自由度５
• 系列５＝自由度１０

自由度１の波形は系列１です。4.29なので、この位置になります。自由度が上がれば上がるほど波が変わっていくので、ｐ値の面積は大きくなるのがイメージできますよね。

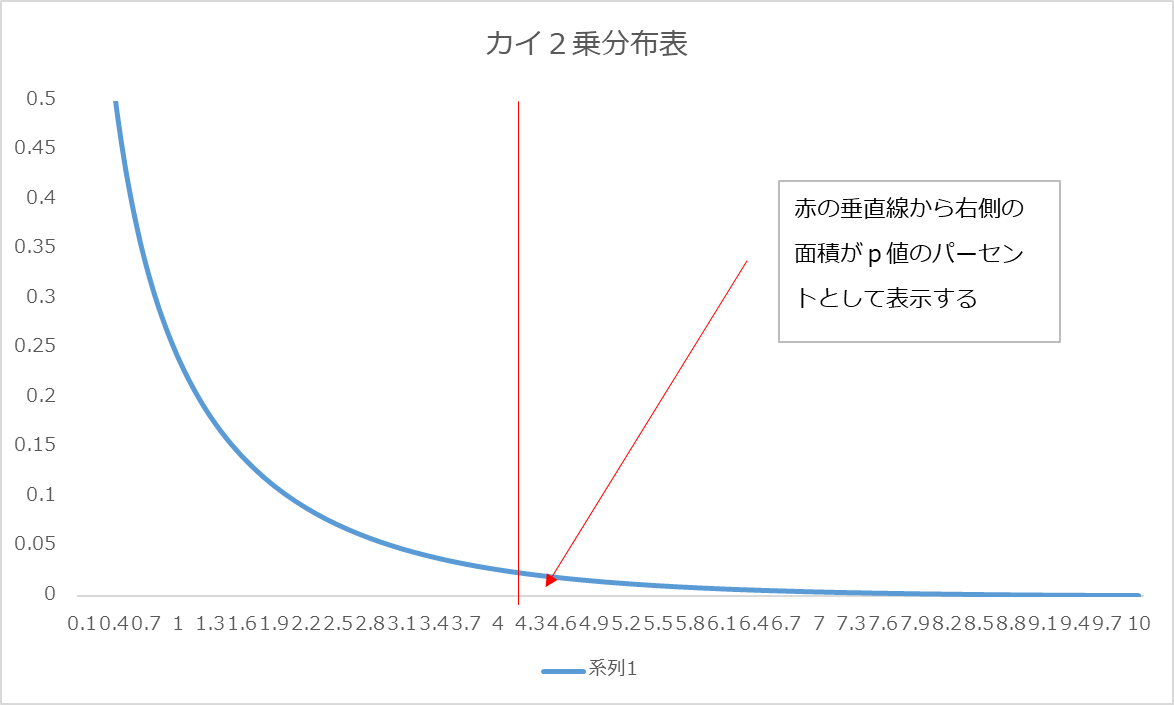
CHISQ.TEST関数で求めたｐ値は「約3.8％」でした。

この％は、この曲線が描く図形の面積を100％とした場合、赤垂線で区切られたところから右側の面積が「約3.8％」という意味になります。

正規分布で１σの範囲が約68％の部分だよ、という説明を思い出していただければと思いますが、カイ２乗検定のｐ値は、自由度によって描かれたカイ２乗分布表の面積を求めているということになります。

この面積が５％を超えると、その差は偶然だよ、ということですね。

CHISQ.DIST.RT関数

先ほどのカイ２乗値と自由度をCHISQ.DIST.RT（カイスクエア・ディストリビューション・ライトテイルズ）関数を用いると、その面積を出すことができます。

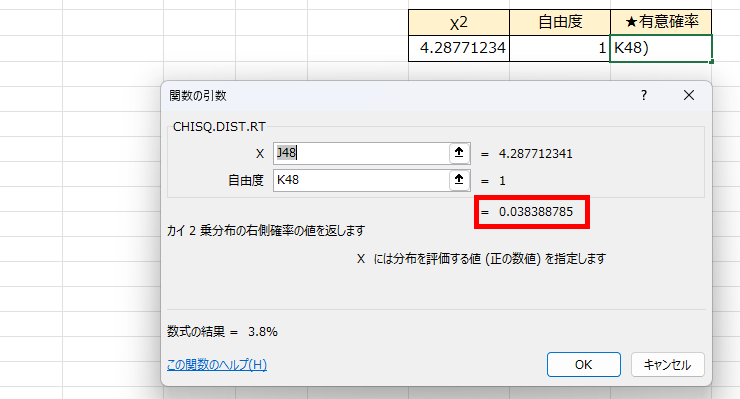
ここまでは覚えなくてOKですよ。

ただ、CHISQ.TEST関数はカイ２乗値を求めて、自由度が分かったら、CHISQ.DIST.RT関数で面積を求められる結果を一気にやっているんだ、ということがわかっていただけるだけで十分です！

まとめ

今回の記事では、カイ２乗検定の「中身」を学びました。

• カイ2乗値は (観測値 − 期待値)² / 期待値 の合計
• 自由度は (行 − 1) × (列 − 1)
• 昔はカイ2乗分布表で判定していた
• 今は CHISQ.TEST が一瞬で p値を返してくれる

統計学は昔の計算方法を知ると、なぜ今の関数が便利なのかもよくわかります。

次の記事では、実際に Excel の計算過程をひとつずつ再現しながら、
「Excel が裏で何をしているのか？」を丁寧に解説します。

いよいよ完全理解編に入るよ！ゆっくりついてきてね！

最終確認日：2025年11月23日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！