カイ2乗検定とは?
それでは、いよいよカイ2乗検定のお話となります。原因となる変数が質的変数で、結果となる変数も質的変数、このパターンの分析です。
- 入口にポスターを貼ったかどうかで、販売数に差が出たのか?
- 平日と土日で、エコバッグ利用率は変わっているのか?
こういった質的同士の関連性を確かめる分析 が、今回紹介する カイ2乗(χ²)検定 です。
Excel には CHISQ.TEST(カイ・スクエアテスト) という関数が標準で備わっており、高度な計算式を知らなくても p値だけを簡単に算出できます。
こちらの記事では、カイ2乗検定の基本と、Excelでの求め方を学習していきましょう。
この記事で学習できること
- カイ2乗検定とは何か
- Excel でカイ2乗検定(独立性の検定)ができること
- CHISQ.TEST 関数の使い方
- サンプルデータを用いた p値の算出

初心者の方でも理解できるように、Excel を使ったシンプルなカイ2乗検定の使い方を学びましょう。ここは Excel が一番!
カイ2乗検定とは?
カイ2乗検定(χ²検定)とは、「2つの質的変数に関連があるかどうか」 を調べるための統計手法です。重要なのは、この検定が…
- 平均値の差
- 数値の大小
ではなく、質的変数(カテゴリー)同士の関連性だけを見るという点です。
具体的には、観測された値(実際のデータ)と期待される値(期待値)のズレが大きいかどうかを判断し、そのズレが偶然とは考えにくいレベルかどうかを p値 で評価します。
まあ、そういってもピンとこないので、実際に読み進めていってください。
今回使用するサンプルデータ
① S社・A社 × ポスターの有無
| 入り口にA社のポスター | S社の販売数 | A社の販売数 |
|---|---|---|
| A社のポスターなし(通常営業) | 118 | 65 |
| A社のポスターあり | 120 | 101 |
A社のキャンペーン戦略で、スーパーの入り口にA社のポスターを貼ったことに効果があったかどうかを確認していきたいと思います。
一見すると、A社の販売数はポスターありだと伸びていますよね。意味のある差が起きたかどうか?(効果があったかどうか?)を統計学的に調べていきます。
② エコバッグ × 利用曜日
| 曜日区分 | エコバッグ | レジ袋 |
|---|---|---|
| 平日(平均値) | 140 | 76 |
| 土曜 | 111 | 176 |
| 日曜 | 110 | 185 |
土・日にやらたとレジ袋がなくなっていくことを従業員からのヒアリングで伺い、実際にどれくらいレジ袋が出ているのかを集計した結果です。
平日はなぜエコバック率が高く、土日はレジ袋率が高くなるのか? この現状は偶然なのか必然なのかを p値 で確認していきましょう。
どちらも「行 × 列」で構成されたクロス表(クロス集計表)」 になっているため、カイ2乗検定が適用できます。

クロス表が作れたら、カイ2乗検定が使える合図だよ!
Excel でカイ2乗検定をしてみよう
Excel の CHISQ.TEST 関数を使うだけで p値 が求められます。まず、この関数をマスターすることを最初の目標としてください。
関数の中身は、時間のある時にゆっくり覚えればいいと思います(次の記事からどんどん詳細になっていきます)
① 下準備をする
まず、合計値をそれぞれ算出します。
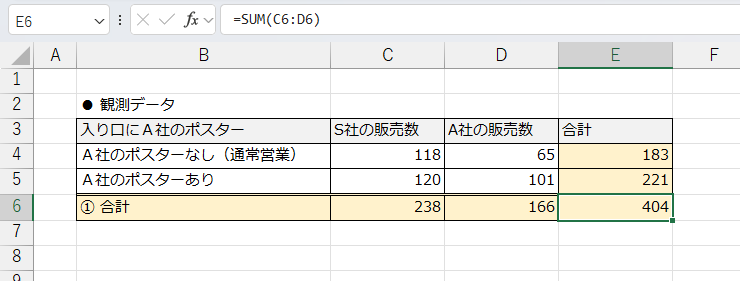
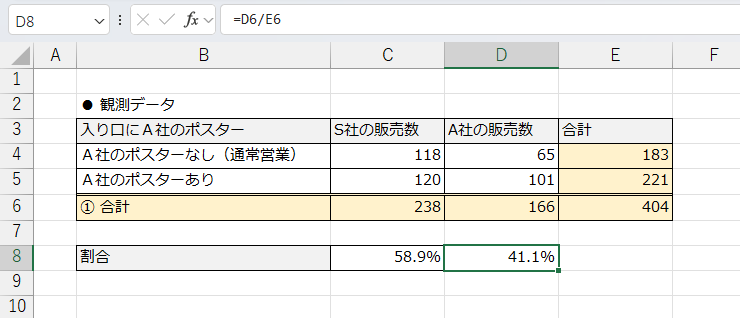
次にこのデータを参考にそれぞれの会社の商品が選ばれた確率を求めます。
- S社の販売確率は「238÷404」
- A社の販売確率は「166÷404」
このようになります。
続いて、期待値を求めます。
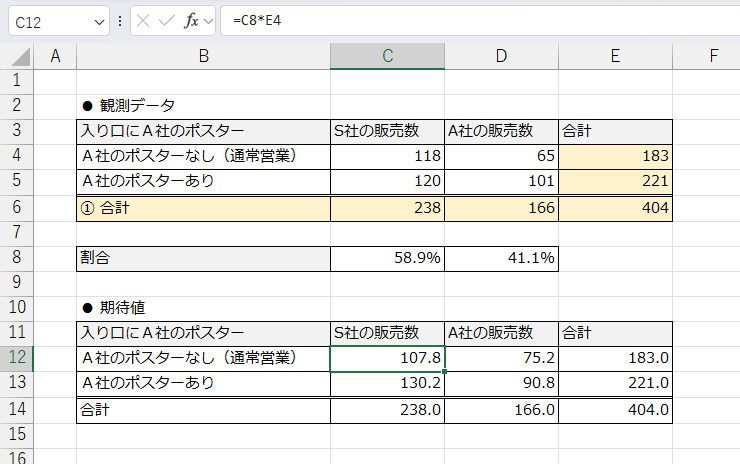
S社の商品を選ぶ確率×A社のポスターなしの合計になるわけです。数式が見えるように表示しておきます。
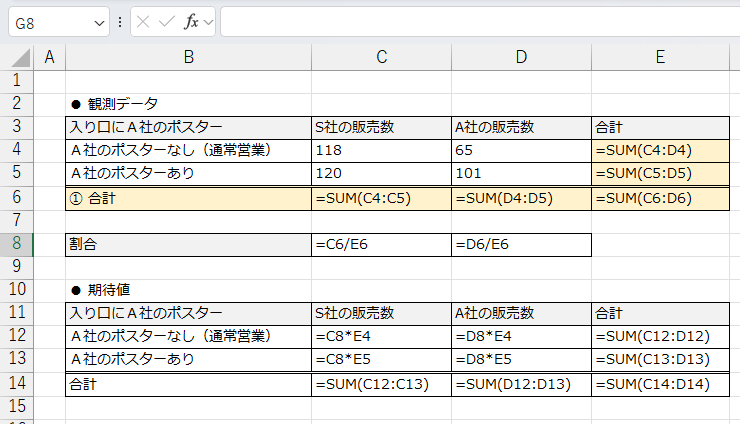
これで準備完了です。
手順②:CHISQ.TEST関数を使う
関数ライブラリの中の「その他の関数→統計」の中にCHISQ.TEST関数があります。
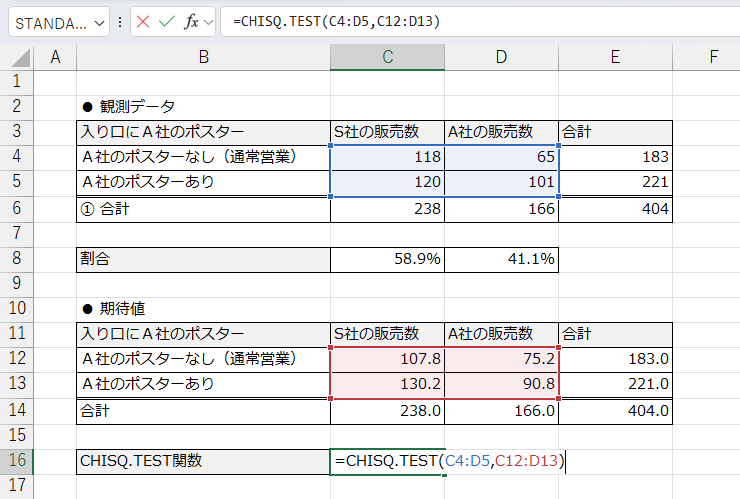
=CHISQ.TEST(観測範囲, 期待値範囲)
関数を入力すると、Excel が
- 行合計
- 列合計
- 全体の合計
- 期待値の算出
- χ²値
- 自由度
- 最終的な p値
をすべて内部で自動計算し、p値だけを返してくれます。

まずはCHISQ.TEST関数の使い方をマスターさえすれば、カイ2乗検定は簡単にp値まで算出できますので、この計算フローを確実に覚えておいてね! 他の細かい内容は全然ゆっくりでOKです!
実際にp値を確認してみる

p値が 一般的な有意水準 5%(0.05)より小さいため、ポスターの有無と売上構成には関連があると判断できます。
つまり、この結果は偶然ではなく「A社のポスターあり」によって、A社の販売数は伸びたことが、統計学的にも判断できるという結果です。
数字を武器にできますので、ただ単に「販売数が伸びた!」というよりも「統計学的にも有意に表れているので、効果は確かだ!」と強く主張することができますよね。
エコバッグ × 利用曜日の例
もう一つの方もざっと解いてみました。こちらは皆さん自身で復習もかねてやってみてくださいね。答えだけ載せておきます。
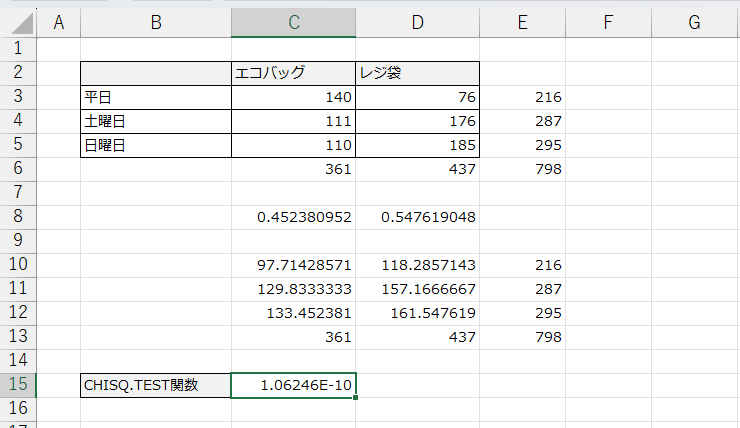
1.06246E-10 というのは、10の-10乗ということ。
つまり、0.000000000106246…という値を意味しています。整数値を含めた0が10個続いて、106246…と数字が続きますよというExcelの指数表示なんですね。
つまり、p値が0に限りなく近い値であるため、「曜日によってエコバッグ利用率は異なる」と結論づけられます。
その結果から、以下のような推察ができるわけですね。
- 通常の買い物客の違い
- 平日には主に主婦やリピーターのお客様が来店することが多く、環境に配慮してエコバッグを利用する意識が高いかもしれません。主婦層は買い物の頻度が高く、エコバッグを使う習慣が定着している可能性があります。
- プロモーション戦略
- 土日にエコバッグを利用することで割引が受けられるイベントや、ポイントを多くもらえるキャンペーンを実施することで、エコバッグの利用を促進できるでしょう。
- 家族連れのお客様
- 土日には、家族全員分の買い物が増え、大量の買い物が多くなるため、エコバッグだけでなくレジ袋も必要になる傾向があるかもしれません。また、週末に多い家族連れの男性客(お父さん)がレジ袋を使うケースが多い可能性があります。
データ分析は、基本的に結果しかわからないので、その情報をどう読み取ってアクションを取るか? が腕の見せ所になるというわけですね。

買い物袋の事例は、ぜひ皆さんもExcelを立ち上げて、同じように計算結果を求めてみてくださいね!
まとめ
カイ2乗検定の本質は、
- 観測値と期待値のズレ
- ズレが偶然なのか有意なのか
- p値で判断する
という流れです。Excel が自動で計算してくれるため、実務で使うだけなら CHISQ.TEST 関数を知っていれば十分です。
次の記事では、
- Excel が計算している期待値の求め方
- カイ2乗統計量の考え方
- 自由度の意味
- p値が導かれる流れ
など、カイ2乗検定の「中身」を丁寧に解説します。

今回の記事で p値の算出まで理解しておけば、次のステップにスムーズに進めます。この分析はとても難しいので、一気に理解しようとすると沼にはまるので気を付けてくださいね
最終確認日:2025年11月23日



