母平均を推察する標準誤差

受講生からの講座レビューを日々受け取っている私にとって、標準誤差（ひょうじゅんごさ）という値は、不確実なデータから信頼する情報を引き出すための重要な指標です。

アンケートデータで収集して現状どういう評価がされているのかを把握するための強力な値ですので、ここは確実にマスターしておきましょう。

英語では「Standard Error（スタンダード・エラー）」と呼ばれ、「SE」と略されることもあります。漢字も読み方も「標準偏差」と間違えやすいので注意してください。

それでは標準誤差が何故重要なのか、学習してきましょう。

実際に数字を追っていないと伝わりにくいのですが、標準誤差の値を見るだけで、このコンテンツはOKかNGかを瞬時に判断できます

標準誤差

標準誤差は、母集団の平均値を標本に基づいて推定する際に用いられる指標です。といっても難しいですよね。シンプルな５段階評価で例えてみましょう。

私の講座を受講した30人から得られたレビューの平均値が「4.3」だったとします。

標準誤差が「±0.3」と算出された場合、母集団の平均レビュー値は「4.0～4.6」の間にあると推定できます。

つまり、ポジティブに考えて「4.6」、ネガティブに考えて「4.0」ということです。ネガティブに考えて「4.0」という高水準であるならば、現段階では成功中と言えるでしょう。

この推定値は集計時のサンプルデータに基づくもので、将来的に変わる可能性があります。だから、成功中だ！　やった！　と安心して気を抜いてはいけないということですね。

しかし短期間（３カ月程度）は、この範囲内に収束すると考えることができます。私自身もそういう値として扱っています。日々の評価を見る際の大きな安心材料となるわけです。

先に計算方法をご紹介しますので、そのあと実際にExcelで確認していきましょう。

標準誤差の計算方法

標準誤差の計算式は、以下のとおりです。

標準偏差は、平均値からのばらつきを示し、データの件数を平方根で割ることで、サンプルサイズの影響を適切に考慮します。

例えば、高校３年生男子の平均身長が170cm、標準偏差が5cm、サンプルサイズが25人の場合、標準誤差は「５÷√25」→「５÷５」で1cmになります。つまり、全国の男子高校３年生の平均身長は、169cmから171cmの範囲に収まるだろうと推定できます。

これを推定母平均と呼びます

標準偏差は分散の平方根であることを思い出してね。

√データの件数という表現は、標準偏差を分散に置き換えると「分散 ÷ データ件数」と同じ意味になります。

ただ、分散だと値が大きく扱いにくいため、一般的には「標準偏差 ÷ √データ件数」という表現が使われています。

講師の講座レビューデータで解析

こちらのワークシートをご覧ください。私のExcel講座600件分のレビューを集めました。5段階評価の数値データは「順序尺度」で「量的変数」として分類されます。

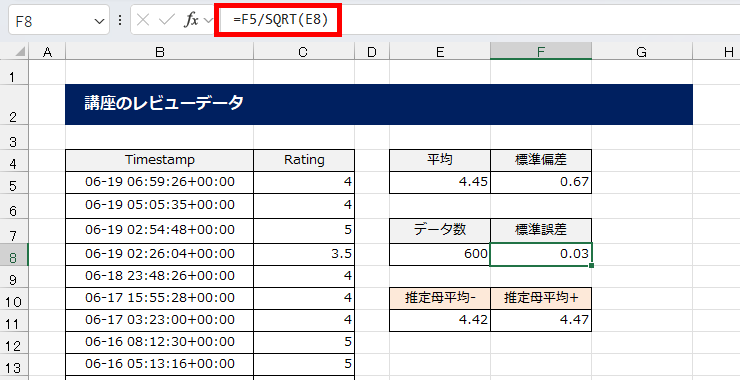
標準誤差は、標準偏差÷SQRT（データの件数）で求めています。SQRT（スクエアルート）関数は平方根を求めてくれる関数です。

• 平均レビューが「4.45」
  • 600件分の平均値です
• 標準偏差が「±0.67」
  • 約68％の人たちが評価するばらつき範囲
• 標準誤差が「±0.03」
  • 推定母平均
    • ネガティブな推定母平均が「4.42」
    • ポジティブな推定母平均が「4.47」

悲しいことに、稀にレビュー１をもらうこともありますが、全体の推定値が4.42～4.47の範囲なので、外れ値として認識しても問題はなさそうです。

ただし、繰り返しになりますが現時点の評価値であって、未来永劫この推定母平均の範囲がこのままであることはありません。レビュー１が多くなれば、すぐに標準誤差の値は大きくなり、平均値は１に向かって崩れていってしまうでしょう。

現在の講座クオリティで、だいたい３カ月先ぐらいまではこの値の範囲内で安心していいだろうという程度のものです。継続しないとですね。

だから、ここまでで表現している推定母平均は「現時点で推定される母平均の範囲」ということになります。

標準偏差をデータ件数の平方根で割る

標準偏差はデータ全体のばらつきを表す指標で、サンプル数が増えてもこの値は変わりません。しかし、サンプル数が増えると「平均値の精度」はどんどん高まっていきます。

いわずもがな、サンプル数が増えるほど、平均値は母集団の平均に近づく性質があるためです。ただし、ここで注意が必要です。

サンプル数が２倍になっても、平均値の信頼性が２倍になるわけではありません。サンプル数が４倍になっても、信頼性は４倍になりません。

ちょっと難しい言い回しなのですが、平均の精度は「サンプル数の平方根に比例して向上すること」が数学的に分かっています。

例えば、先ほどの高校生の身長の例では、サンプル数を25人から100人に増やしても、平均の精度は４倍ではなく２倍しか良くなりません。サンプル数を４倍にしても、信頼性が上がるのは平方根の２倍だけだからです。

このように、サンプル数が増えるほど平均値の推定は正確になりますが、その向上のスピードは「サンプルサイズの平方根」によって緩やかになっていきます。

ですので、サンプル数が少ないうちは標準誤差の動きも大きいわけですが、サンプル数が多くなってくると、標準誤差の値も大きく変わらなくなってくるという点がポイントです。

私の講座レビューデータの標準誤差は「0.03」でした。もう600件追加しても、この数値は微動だにしないでしょう。

まとめ

標準誤差は、レビューを受けている人たちにとって非常に強力な値だと信じています。

ただ、繰り返しになりますが、標準誤差は現時点で計測した推定される母平均であり、未来永劫この値が留まらないということを覚えておいてください。

私自身も平均レビュー4.3を維持するために、わかりやすい指導を心がけていきますね。

定期的に標準誤差をチェックするのは大切なことですね！

最終確認日：2025年11月19日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！