基本統計量

こちらの記事では、統計学における「基本統計量」を学習していきます。

基本統計量とは、データから情報を引き出す分析作業において、重要な指標を示す代表的な値の集まりのことを指します。

簡単な値からスタートしていきましょう！

まず、この６つの値を学習しましょう。

平均値・中央値・最頻値を、一般的に代表値と読んだりもしています。

それでは「平均値」から解説を始めていきましょう。

① 平均値

ご存じの方も多いと思いますが、平均値の求め方からおさらいです。

統計学の用語では別名があり、相加（そうか）平均とも呼びます。

平均値には、相乗（そうじょう）平均や調和（ちょうわ）平均など、さまざまな種類がありますが、それらと区別するために相加平均と呼ぶこともあります。

けれども、一般的に平均値といったら相加平均を指します。ここでは、一般的な表現として平均値という言葉を使って進めますね。

平均値は、データの合計を個数で割る計算方法で求められますが、言葉を分解して考えるとさらに平均値を理解することができます。

平らに、均（なら）す、値。それが平均値です。

以下のキャプチャのように、ブルドーザーが平均線上に土を平らに均していくようなイメージです。

大きな溝があれば、そこに土を埋めなければいけません。また、大きな山があればその山を崩して、平らに均していきます。

データの中で、ひと際大きな溝・大きな山のことを「外れ値」と呼び、平均値はこの外れ値に対して影響が出やすい値とも言えます。

最後に、平均値の英語読みの確認です。

Excelでは、平均の関数が「AVERAGE（アベレージ）関数」のため、アベレージという言葉をよく聞きますが、平均は英語読みで「MEAN（ミーン）」といいます。

統計の書籍を紐解いていると、この単語もよく出てきますので、併せてMEANという単語でも「平均」というキーワードを紐づけておきましょう。

10人参加の飲み会で、3人がドカ食い＆ドカ飲みしてしまったら、お会計を割り勘にしてしまうと残り7人がムッとしますよね

② 中央値

データを昇順（または降順）に並び替えた、真ん中の値が中央値です。

中央値は、データ群の中に外れ値が含まれていたとしても、中央値は計算されずに抽出されるため、外れ値の影響を受けにくい値として扱われます。

そして、平均値と比較材料となる値にもなります。

データ群が奇数の場合は、きちんと真ん中の値が抽出されますが、データ群が偶数の場合は、真ん中の値が２つ存在します。

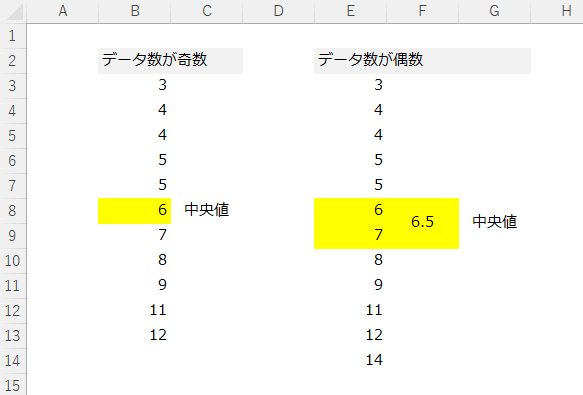
その２つの値の平均値となるため、データ群が偶数の場合だと実測データが出てこない可能性がある、ということを抑えておいてください。

中央値を実データで捉えたいのであれば、集めるサンプルデータ数は奇数にしたほうがいいでしょう。

しかし、データ群が奇数でも偶数でも、中央値としての性質はさほど失われないので、絶対にサンプルデータ数は奇数でなければならない！　ということはありません。

また、平均値と中央値が近しい値であれば、そのデータにばらつきはないと推定もできます。いろいろな値を参考にして最終結論を出すわけですが、代表値の中でも中央値と平均値は比較してみることが多いです。

中央値は、英語読みで「MEDIAN（メジアン）」と呼びます。ExcelではMEDIAN関数を使って、中央値を求めることができます。

使い方はAVERAGE関数と全く同じなので、試してみてくださいね。

真ん中の値ということは「50％位置がわかる」というのがポイントです。平均値が2,000円、中央値が900円だったら、50％位置にいる人が900円なので、平均値は大きな外れ値に引っ張られているということがわかりますよね

③ 最頻値

出現頻度が一番多い値のことを指します。「3,4,4,5,5,5,6,6」というデータ郡であれば、最頻値は「５」になります。

また「3,4,5,6,7,8,9,10」のように、最頻値の値が見つからない場合は 「最頻値なし」と記載します。 Excelなどのアプリケーションソフトでは「#N/A（ノーアサイン）」というエラーが表示されます。

最頻値も中央値と同じで、外れ値の影響を受けにくい値です。

ただし、実際の分析では最頻値が出ない場合もありますので、平均値と中央値に比べて情報量は多くないという点がポイントです。

そのため「100万〜200万、200万〜300万……」「30代・40代・50代……」といった区間（これを階級といいます）に置き換えて、どこの区間が一番件数が多いのか？　ヒストグラムというグラフを使って最頻値を把握するほうが多いでしょう。

このヒストグラムについては、度数分布表の話に入ってからご説明いたします。ですので、いまは基本統計量の代表値である「最頻値」をまず覚えておいてください。

最頻値の英語読みは「MODE（モード）」といいます。

④ 最大値

データ群の中で、最も大きな値を「最大値」といいます。シンプルですが、これも代表値のひとつです。英語読みは「MAX（マックス）」。

これは、特に説明は不要ですね。データ全体の上限値を知ることができます。

⑤ 最小値

その逆に、データ群の中で最も小さな値を「最小値」といいます。英語読みは「MIN（ミニマム）」。これも説明不要な代表値と言えるでしょう。

ExcelではMIN関数を「ミニマム関数」と読むことが一般的ですが、データベースなどのSQLを学習しているときのMIN関数は「ミン関数」と読むことが多いです。

なんだか不思議ですよね。データ全体の下限値を知ることができます。

⑥ レンジ

データの最大値と最小値の差を「レンジ（範囲）」といいます。

データの振れ幅です。上限と下限の範囲を知ることで、どれくらい繁忙期と閑散期で差があるのか？　などを確認することができます。

レンジが広すぎれば、データは全体的に散らばっている、または外れ値が存在していると判断できるわけです。こちらは「ばらつきの指標」として用いられます。

英語読みでは「RANGE（レンジ）」と読み、レンジは「Data Range（データ・レンジ）」と呼ぶことが多い印象です。

Excelを含むほとんどのアプリケーションではRANGE関数というものは存在しないため、最大値と最小値の差分によりレンジを求めます。

他のプログラムでも、標準の関数にはありませんよね。代表される値なのに、なんだか不思議…

【参考】貯蓄現在高等級 2023年

家計調査報告（貯蓄・負債編）－2023年（令和５年）平均結果－（二人以上の世帯）

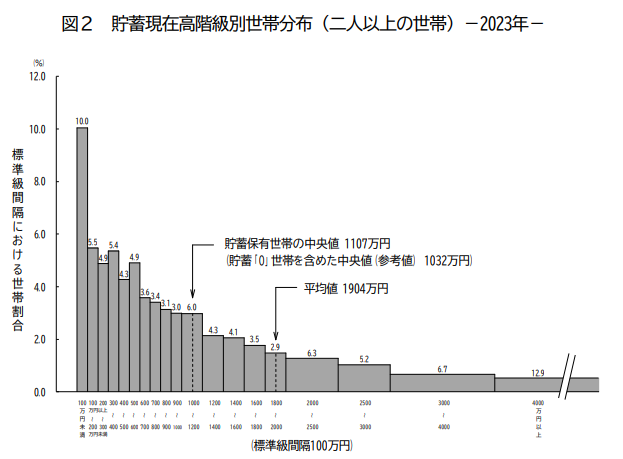
平均値・中央値・最頻値の説明において、こちらのグラフ（貯蓄現在高等級別世帯分布表）がとても参考になります。

こちらの表を見ると、２人以上の世帯で、すれ違った人の50％は、1,107万円の貯金があることを意味しています。平均値が1,904万円というのは、億を持っている人がいるため、それに引っ張られているという意味です。

まとめ

基本統計量の①平均値、②中央値、③最頻値、④最大値、⑤最小値、⑥レンジを学習しました。

まだまだ基本統計量として見るべき値は残っているのですが、ここで記事を区切ります。

次の記事は、標準偏差を説明している統計学の最初のハードル「標準偏差（次の講座）」に進んでください。こちらも重要な基本統計量です。

次は統計でも一番重要な「標準偏差」に進んでいくよ！

最終確認日：2025年11月19日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！